Linear regression fits a linear model through a set of data points to estimate the relationship between a target outcome label and one or more feature variables in order to predict a numeric value. The output y (label) can be estimated as a straight line that can be visualized as:
y = intercept + ci * xi + Error
Where xi are the input variables (features), and the parameters ci, intercept, and Error are the regression coefficients, the constant offset, and the error respectively. The coefficients ci can be interpreted as the increase in a dependent variable (y label) for a unit increase in the respective independent variable (x feature). In the simple example below, linear regression is used to estimate the house price (the y label) based on the house size (the x feature).
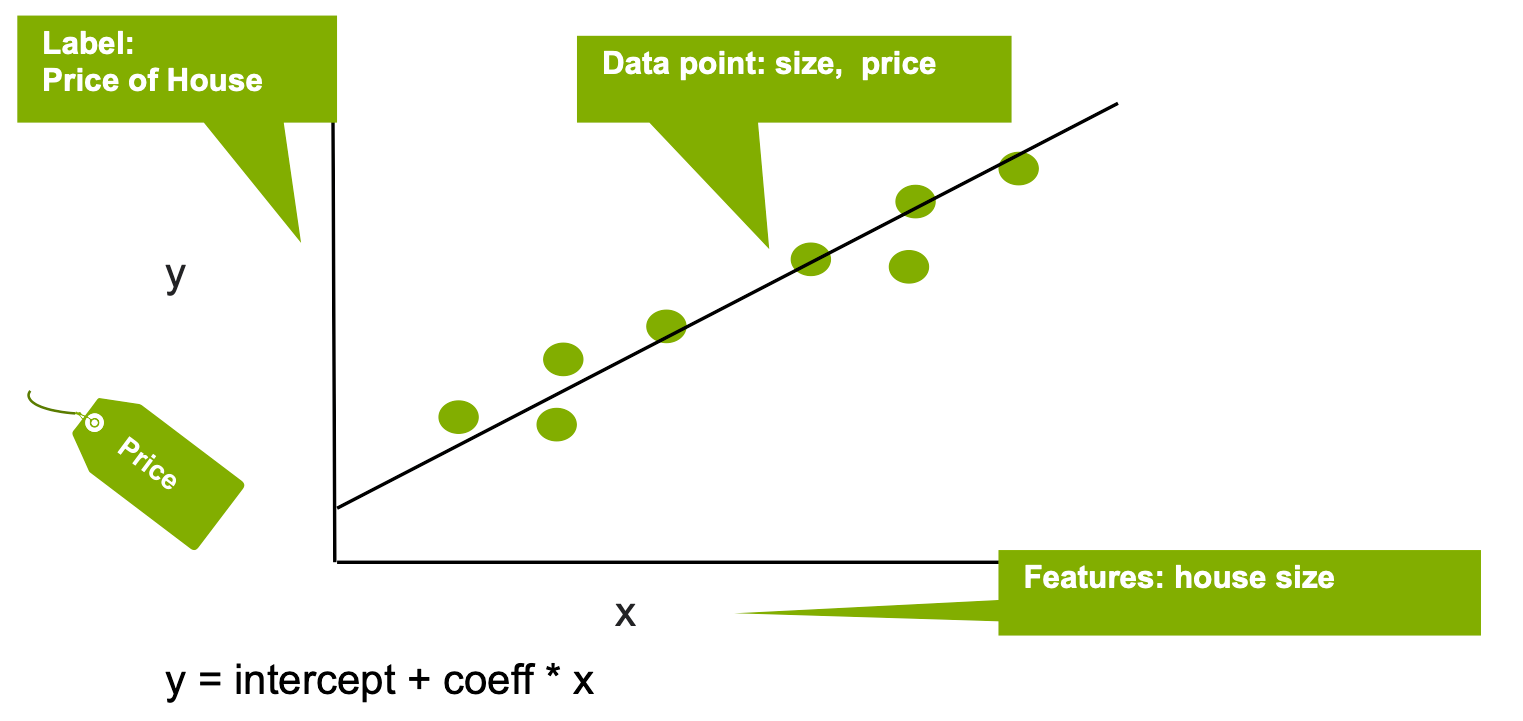
The distance between the x and y points and the line determines the strength of the connection between the independent and dependent variables. The slope of the line is often determined using the least squares method in which the sum of the squares of the offsets of points on the curve is minimized.
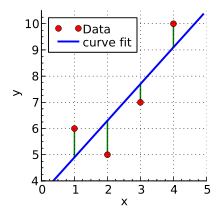
Source: Wikipedia
There are two basic types of linear regression—simple linear regression and multiple linear regression. In simple linear regression, one independent variable is used to explain or predict the outcome of a single dependent variable. Multiple linear regression does the same thing using two or more independent variables.
Regression is often used for predicting outcomes. For example, regression might be to find the correlation between tooth brushing and tooth decay. The x-axis is the frequency of cavities in a given population and the y-axis is the frequency with which people in that population brush their teeth. Each person is identified by a dot on the chart representing their weekly brushing frequency and the number of cavities they have. In a real-world case, there would be dots all over the chart, as even some people who brush frequently get cavities while some people who don’t brush very often are spared from tooth decay. However, given what is known about tooth decay, a line that comes closest to touching all the points on the chart will probably slope down and to the right.
One of the most useful applications of regression analysis is the weather. When a strong correlation can be established between variables–such as ocean temperatures in the southeastern Atlantic and the incidence of hurricanes–a formula can be created to predict future events based upon changes in the independent variables.
Regression analysis can also be useful in financial scenarios such as predicting the future value of an investment account based upon historical interest rates. While interest rates vary from month to month, over the long term, certain patterns emerge that can be used to forecast the growth of and investment with a reasonable degree of accuracy.
The technique is also useful in determining correlations between factors whose relationship is not intuitively obvious. However, it’s important to remember that correlation and causation are two different things. Confusing them can lead to dangerous misassumptions. For example, ice cream sales and the frequency of drowning deaths are correlated due to a third factor–summer–but there’s no reason to believe that eating ice cream has anything to do with drowning.
This is where multiple linear regression is useful. It examines several independent variables to predict the outcome of a single dependent variable. It also assumes that a linear relationship exists between the dependent and independent variables, that the residuals (points that fall above or below the regression line) are normal, and that all random variables have the same finite variance.
Multiple linear regression can be used to identify the relative strength of the impact of independent upon dependent variables and to measure the impact of any single set of independent variables upon the dependent variables. It’s more useful than simple linear regression in problem sets where a great many factors are at work, such as forecasting the price of a commodity.
There is a third type called nonlinear regression, in which data is fit to a model and expressed as a mathematical function. Multiple variables are usually involved and the relationship is represented as a curve rather than a straight line. Nonlinear regression can estimate models with arbitrary relationships between independent and dependent variables. One common example is predicting population over time. While there is a strong relationship between population and time, the relationship is not linear because various factors influence changes from year to year. A nonlinear population growth model enables predictions to be made about population for times that were not actually measured.





